In veel gevallen zijn stroommetingen zonder DC-component nuttig. Het betreft dan meestal CT’s (current transformers, stroomtransformatoren) voor wisselstroom. Dit artikel gaat over het ontwerp van stroomtransformatoren voor gemiddelde tot hoge frequenties, die heel eenvoudig te bouwen zijn. De gepresenteerde formules zijn ook geldig voor AC-nettransformatoren.

Figuur 1. Een close-up van mijn HF-stroomprobe.

Het principe van de probe

De probe van figuur 1 is ontworpen om tot 50 A piek te meten in een frequentiebereik van 7 kHz tot tientallen MHz. Het schema in figuur 2 is vrij eenvoudig: de draad waardoorheen de stroom moet worden gemeten, wordt door de ringkern gevoerd; dat is een gewone Amidon-kern type FT 82-43 die goed presteert tot ten minste 50 MHz.

Figuur 2. Het simpele schema van mijn HF-stroomprobe.

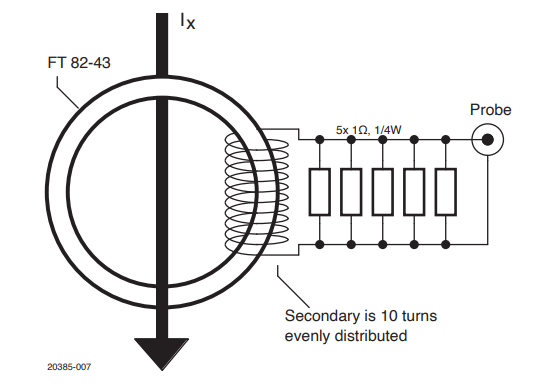
De secundaire wikkeling bestaat uit tien gelijkmatig over de kern verdeelde windingen. Gebruik indien mogelijk een niet te dunne draad, maar dat is niet verplicht. Door de wikkelverhouding van 1:10 is de maximale stroom in de secundaire 5 A piek.

De secundaire winding is belast met 0,2 Ω in de vorm van een parallelschakeling van vijf weerstanden van 1Ω. Bij een piekstroom van 5A bedraagt de piekspanning over deze weerstanden 1V, prima geschikt voor metingen met een oscilloscoop. Voor een sinusvormige stroom is de gemiddelde dissipatie in de weerstanden R∙I2=R∙Ip2/2=2,5 W of 0,5W per weerstand. Een continue sinusvormige stroom van 50 Ap kan alleen worden gemeten met weerstanden van 0,5W of groter. Maar bij gepulste golfvormen of als er zeer korte metingen worden verricht, zijn weerstanden van 0,25W voldoende. Dat was mijn keuze omdat ik het ontwerp compact wilde houden voor betere HF-prestaties. Eerlijkheidshalve moet ik ook toegeven dat ik deze weerstanden toevallig bij de hand had...

Inschrijven
Schrijf u in voor tag alert e-mails over Current Probe!

Gebruik

Figuur 3 toont een typische toepassing met een oscilloscoop-probe en een BNC-adapter voor probes. De schakeling kan ook worden gebruikt met een directe coaxverbinding met de ’scoopingang, omdat 1Vp ideaal is voor gebruik met een oscilloscoop in 1x-modus: in dit geval wordt het gebruik van een korte kabel aanbevolen om reflecties in de betreffende frequentieband te voorkomen, omdat de coax aan beide zijden niet correct is afgesloten. Nog beter is het om de coaxkabel aan ’scoopzijde af te sluiten met zijn karakteristieke impedantie. Veel moderne oscilloscopen bieden de mogelijkheid om de ingangsimpedantie op 50Ω in te stellen, zodat dit bijzonder gemakkelijk is. In dit specifieke geval moet men bedenken dat de meting enigszins verkeerd geschaald zal zijn, vanwege de parallelschakeling van de 50Ω belasting en de 0,2 Ω van de probe (de totale weerstand wordt 0,1992 Ω, wat een schaalfactor geeft van 50,2 A/V).

Figuur 3. De HF-stroomsonde in de praktijk.

Wat moet worden vermeden, is de probe van de ’scoop rechtstreeks met de klemmen op de weerstanden aan te sluiten zonder gebruik te maken van de BNC-connector, want bij het meten van hoge HF-stromen zal zelfs de minimale niet-afgeschermde lus in de probes artefacten toevoegen aan de metingen.

Berekeningen

Het ontwerp van de stroomtransformator is niet ingewikkeld, maar enkele elektromagnetische formules zijn onontkoombaar. Eerst de belastingsweerstand RL, die zo klein als praktisch mogelijk moet zijn om het erdoor geïntroduceerde vermogensverlies te minimaliseren. De te meten kring ‘ziet’ minstens R∙n2, waarbij n de wikkelverhouding is (1:10) en R de som van RL (0,2 Ω) en van de secundaire draadweerstand (enkele mΩ). Zoals al opgemerkt, is het van groot belang dat de secundaire zijde gelijkmatig wordt gewikkeld, omdat de te testen kring anders enige strooi-inductie in serie vertoont. Aan de andere kant, als we een te kleine waarde voor RL kiezen, zullen we ook een zeer kleine te meten spanning hebben, wat ruis in het ’scoopbeeld geeft. Tenslotte moet RL groter zijn dan de weerstand van de secundaire winding.

In mijn geval koos ik 0,2 Ω zodat ik 1 V zou krijgen bij 5 A (50 A op de primaire), wat 2 mΩ toevoegt aan de te testen kring. Het aantal secundaire windingen, n, bepaalt de transformatieverhouding. In het geval van een hoogfrequente CT moet deze n klein worden gehouden om eigenresonantie door strooicapaciteiten in combinatie met een hoge zelfinductie te voorkomen. Bij CT’s voor het lichtnet is de frequentie vrij laag (50 of 60Hz) en daarom is n=1000 een gebruikelijke waarde. Machten van 10 zijn gebruikelijk, zodat de stroom-transformatieverhouding eenvoudig blijft, maar andere waarden zijn mogelijk.

De hoogste bruikbare frequentie voor een ferriet ringkern-CT hangt af van de:

  • prestaties van het ferrietmateriaal;
  • eigenresonantie van de secundaire wikkeling;
  • weerstands-zelfinductie (weerstand zelf en aansluitingen).

Een ontwerp als het mijne kan gemakkelijk tot enkele tientallen MHz functioneren indien een geschikt ferriet, zoals het materiaal ‘43’ van Amidon/Fair-Rite, wordt gebruikt. Kernen met hoge permeabiliteit voor EMI-onderdrukking kunnen ook worden gebruikt, maar dan met een veel lagere maximale frequentie. Kernen met een lage permeabiliteit zoals worden gebruikt voor vermogenssmoorspoelen en hoge-Q-spoelen zijn niet aan te bevelen, omdat hun zelfinductie per winding te laag is, hetgeen van invloed is op het volgende punt.

De keuze van de ferrietkern is ook van invloed op de laagste bruikbare frequentie, en wel om twee redenen:

  • voor een goede meting moet de reactantie van de secundaire veel groter zijn dan R, omdat deze ook als belasting werkt. Aangezien voor de reactantie geldt X=2π∙f∙L, heeft dit gevolgen voor de lagere frequenties. In de praktijk willen we aan de lage kant X>10∙RL;
  • we moeten verzadiging van de kern vermijden, die optreedt bij hoge stroom en lage frequentie. Verzadiging van ferrieten treedt op bij een fluxdichtheid B=0,25...0,3T, maar om niet-lineaire verschijnselen te voorkomen, moeten we onder 0,2T blijven bij de maximale stroom en de minimale frequentie.

Om beide bovenstaande redenen zijn voor lage bruikbare frequenties met een klein aantal windingen en een hoge stroom grote kernen nodig. De belangrijkste kernparameters zijn AL, de inductantie per winding, meestal uitgedrukt in nH/n2 voor HF-kernen, en de kerndoorsnede S, die gemakkelijk kan worden berekend uit de afmetingen van de kern. In het geval van de kern Amidon FT 82-43 is AL=470nH/n2 en is de doorsnede 24,6mm2 (gemakkelijk te berekenen uit buitendiameter, binnendiameter en hoogte).

De inductantie van 10 windingen is dus 470 nHx102= 47µH (vergeet niet dat de zelfinductie afhangt van n2). Als we aannemen dat X=10∙R≈10∙RL=2Ω, krijgen we (door de formule voor de reactantie om te keren) f>6,8kHz als lage afsnijfrequentie. Dit kan aanvaardbaar zijn of niet, afhankelijk van de toepassing, en een grotere kern, met een grotere AL, zal een lagere afsnijfrequentie hebben. In mijn geval, voor het meten van een ‘muzikale’ Tesla-spoel, was ik geïnteresseerd in frequenties boven 500 kHz, dus deze kern voldeed prima.

Met betrekking tot verzadiging geldt in het sinusvormige regime voor de grootte van het veld B (de magnetische fluxdichtheid) abs(B)=Vp/(n∙2π∙f∙S) is, waarbij Vp de piekspanning over de wikkeling is. Deze vergelijking kan worden afgeleid door de twee uitdrukkingen voor de magnetische flux Φc=L∙I=n∙B∙S gelijk te stellen en I te vervangen door de absolute waarde van de magnetiserende wisselstroom abs(I)=V/(2π∙f∙L). Indien V en n in eerdere ontwerpfasen zijn vastgelegd, is de enige manier om een lagere f te bereiken het gebruik van een grotere S: een grotere torus.

In mijn geval is Vp=1V, n=10, S=24,6mm2 (let op de juiste eenheden), dus hebben we B<0,2T voor f>3,2kHz, wat prima is (althans voor mijn toepassing). Het is misschien verwarrend dat de stroom niet in de berekening voorkomt: hij gaat eigenlijk schuil achter V, omdat we weten dat 1V overeenkomt met 50A.

Verbeteringen

Capacitieve koppeling tussen primaire en secundaire wikkelingen kan metingen verstoren bij de hoogste nog bruikbare frequenties, of zelfs bij gemiddelde frequenties als de primaire geleider een hoge RF-spanning voert.

Het ontwerp kan worden verbeterd door een elektrostatische afscherming toe te voegen die deze capacitieve koppeling voorkomt: in de praktijk wordt de primaire draad daartoe door een klein stukje metalen buis (typisch koper of messing) gevoerd dat verbonden is met de uitgangs-GND van de secundaire wikkeling, zoals te zien in figuur 4. Dit verandert niets aan de magnetische koppeling, maar blokkeert het elektrische veld.

Figuur 4. Verbeterde probe met elektrostatiesche afscherming.

Conclusie

Dit voorbeeld van een HF-stroomtransformator met de belangrijkste ontwerpcriteria bewijst dat deze materie minder complex is dan zij in eerste instantie lijkt. Ik hoop dat de hier gepresenteerde overwegingen en formules nuttig zijn om de omgang met ringkernen te vereenvoudigen, en als basis dienen voor je eigen ontwikkelingen.

Over de auteur

Roberto Visentin is een onlangs gepensioneerde elektrotechnicus die aan elektronica en besturingssystemen voor maritieme toepassingen en onderwaterrobotica heeft gewerkt. Hij is nog steeds actief als freelance consultant, maar heeft nu gelukkig ook meer tijd om hobbyprojecten te ontwikkelen in zijn elektronica-lab thuis.

Vragen of opmerkingen?

Hebt u technische vragen of opmerkingen naar aanleiding van dit artikel? Stuur een e-mail naar de redactie van Elektor via redactie@elektor.com.

Dit artikel is oorspronkelijk gepubliceerd in Elektor Mei & Juni 2023. Word vandaag nog lid van Elektor community!