Kunstmatige intelligentie (AI) en machine learning (ML) zijn hot in de industrie. Dankzij successen die in de pers aan bod zijn gekomen, zoals het feit dat AI de beste Go-spelers ter wereld heeft verslagen [1], en mislukkingen, zoals ongelukken met autonome voertuigen [2], is AI deel geworden van de lingua franca. Hoewel AI en ML zijn gedemocratiseerd dankzij cloud-based tools zoals TensorFlow,  lijken deze enorme krachtige platforms ongrijpbaar als je probeert te begrijpen hoe ML "onder de motorkap" werkt. In deze serie over neurale netwerken gaan we terug naar de basis en verkennen we basisbouwstenen van deze systemen. Onderweg zijn er tal van voorbeelden om uit te proberen, voorbeelden van coole en obscure ML-projecten, en aan het eind zullen we zelfs een Arduino van een brein voorzien. 

Uitdagingen op computergebied

AI en ML zijn dé computeruitdagingen van onze tijd. AI, dat zich richt op het gebruik van computers om menselijke intelligentie na te bootsen, en ML, dat zich richt op patroonherkenning van gestructureerde en halfgestructureerde gegevens, vergen jaarlijks aanzienlijke investeringen, van onderzoekprojecten tot de ontwikkeling van halfgeleidertechnologie en computerplatforms. En dankzij de 'cloud' is de technologie gemakkelijk toegankelijk voor wie zijn ideeën wil onderzoeken en testen.

Maar wat zijn neurale netwerken? Hoe werken al die slimme algoritmen? Hoe leren ze? Wat zijn hun beperkingen? En is het mogelijk om metML te spelen zonder je te registreren voor de zoveelste cloud-service? Dat zijn de vragen die in deze vierdelige serie over neurale netwerken aan de orde zullen komen:

  • Deel 1 - Kunstmatige Neuronen: In het eerste deel van deze serie over neurale netwerken, beginnen we in de jaren 1950 om te kijken naar het vroege onderzoek om een kunstmatig neuron te ontwikkelen. Van daaruit gaan we snel over naar een multilayer perceptron (MLP) software-implementatie die backpropagation gebruikt om te 'leren'.
  • Deel 2 - Logische neuronen: een van de uitdagingen met vroege neuronen was hun onvermogen om de XOR-functie op te lossen. We onderzoeken of onze MLP dit probleem kan oplossen en visualiseren hoe het neuron leert.
  • Deel 3 - Praktische neuronen: We passen onze MLP toe op een deel van het autonoom-rijden probleem: het herkennen van de status van verkeerslichten met behulp van een PC-gebaseerd programma.
  • Deel 4 - Embedded neuronen: We sluiten de serie over neurale netwerken af met embedded neuronen. Als het op een PC werkt, zou het toch ook op een microcontroller moeten werken, nietwaar? Met behulp van een Arduino en een RGB sensor, detecteren we opnieuw de kleuren van verkeerslichten.

    Lui Leren

    Leren is hard werken voor mensen én voor AI. Onderzoek door de TU Berlijn, Fraunhofer HHI, en SUTD liet AI-systemen hun beslissingsstrategieën uitleggen [13]. De resultaten waren verbluffend. Hoewel de AI's allemaal hun taken op bewonderenswaardige wijze uitvoerden, vertoonden zij een adembenemende brutaliteit in hun besluitvorming. Eén algoritme bepaalde correct de aanwezigheid van een schip op een foto, maar baseerde die beslissing op het feit dat er water op de foto stond. Een ander algoritme detecteerde correct dat foto's paarden bevatten, maar baseerde zijn beslissing op een copyright-markering in sommige foto's, in plaats van de visuele kenmerken van een paard te leren.

Neurale netwerken: Een beetje neuronen-geschiedenis

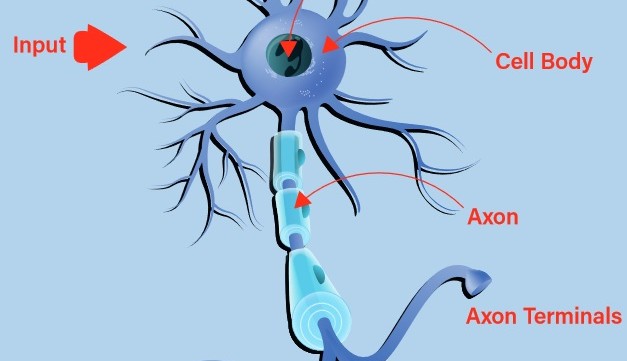
Vroege pogingen om een digitaal, of kunstmatig, neuron te bouwen vonden hun inspiratie in de natuur. Het biologische neuron aanvaardt inputs via zijn dendrieten en geeft het resultaat via zijn axon door aan de axonterminals (figuur 1). De beslissing of een stimulus via de uitgang zal worden uitgezonden, het zogenaamde vuren van het neuron, wordt genomen met behulp van een proces dat activering wordt genoemd. Als de inputs overeenkomen met een aangeleerd patroon, gaat het neuron vuren. Zo niet, dan niet. Het is snel duidelijk dat met ketens van met elkaar verbonden biologische neuronen zeer complexe patronen kunnen worden herkend.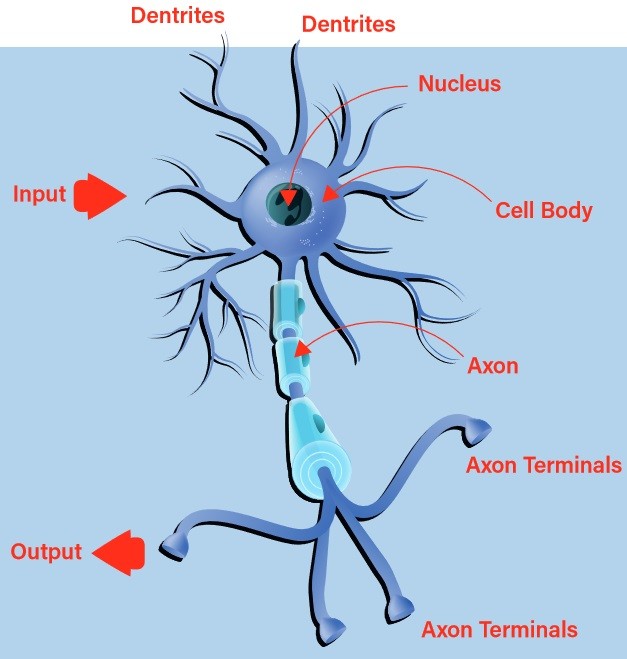
A biological neuron. (Series on Neural Networks)
Figuur 1: Een voorbeeld van een biologisch neuron.
De eerste kunstmatige neuronen die werden ontwikkeld waren McCulloch-Pitts netwerken, ook bekend als Threshold Logic Units (TLU). Dit waren eenvoudige 'beslissingsmachines' die in staat waren de functie van logische poorten na te bootsen. Zij aanvaarden en geven alleen logische waarden 0 en 1. Om hun vermogen tot patroonherkenning te implementeren, moesten voor elke ingang de gewichtswaarden worden bepaald, hetzij mathematisch, hetzij heuristisch. Soms is ook een extra ingang nodig (figuur 2, AND- en OR-functies).
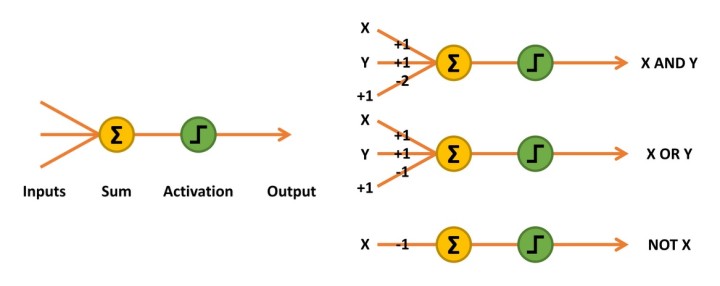
McCulloch-Pitts network sums the inputs multiplied by their weights

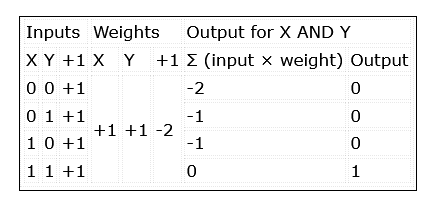
Figuur 2: Het McCulloch-Pitts-netwerk telt de inputs vermenigvuldigd met hun gewichten op en activeert een output van 1 als het resultaat groter of gelijk 0 is.
 
De ingangen van het netwerk worden vermenigvuldigd met hun gewichten bij elkaar opgeteld. De beslissing om een 1 uit te voeren, of te activeren, wordt uitgevoerd met behulp van een lineaire drempelwaarde-eenheid. Indien het resultaat groter of gelijk 0 is, wordt een 1 uitgevoerd. Zo niet, dan is de uitgang 0 (tabel 1).
McCulloch-Pitt network to implement an AND function
Tabel 1: McCulloch-Pitt netwerk om een AND-functie te implementeren.

Perceptrons

De volgende ontwikkelingsfase kwam in de 50-er jaren met het werk van de psycholoog Frank Rosenblatt [3]. Zijn perceptron behield de binaire ingangen en de lineaire drempelwaarde-besluitvorming van de McCulloch-Pitts TLU. De output was dus ook binair 0 of 1. Maar er waren twee verschillen: het drempelniveau (bekend als theta, Θ) voor de besluitvorming over de outputwaarde was instelbaar, en het ondersteunde een beperkte vorm van leren (figuur 3).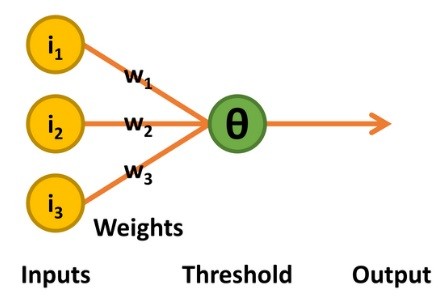
Perceptron introduced a variable threshold level Θ
Figuur 3: De perceptron introduceerde een variabel drempelniveau Θ,
en maakte gebruik van een iteratief leerproces.
Het leerproces werkt als volgt: de perceptron geeft alleen een waarde 1, als de som van het product van de inputs en de gewichten groter is dan theta. Indien de output ten opzichte van de combinatie van inputs juist is, wordt niets veranderd.

Indien een waarde van 1 wordt uitgevoerd terwijl een 0 is vereist, wordt het drempelniveau van theta met één verhoogd. Bovendien worden alle gewichten die horen bij ingangen van 1 verminderd met 1. Gebeurt het omgekeerde, d.w.z. er wordt een waarde 0 uitgevoerd wanneer een 1 vereist is, dan worden alle gewichten die horen bij ingangen van 1 vermeerderd met 1.

De gedachte hierachter is dat alleen de ingangen met waarde 1 kunnen bijdragen tot een ongewenste output van 1, zodat het zinvol is hun invloed te verminderen door hun bijbehorende gewichten te verlagen. Omgekeerd kunnen alleen ingangen met een waarde van 1 bijdragen tot de gewenste output van 1. Als de output 0 is, en niet 1 zoals gewenst, moeten de bijbehorende gewichten worden verhoogd.

In 1958 werd de 'Mark I perceptron' in hardware gebouwd, nadat hij eerst in software was geïmplementeerd op een IBM 704 [4]. Aangesloten op 400 cadmiumsulfide-fotocellen die een rudimentaire camera vormden en gebruik makend van motoren verbonden met potentiometers om de gewichten bij te werken tijdens het leren, kon het de vorm 'driehoek' herkennen nadat het was getraind [5].

De problemen met perceptrons

Hoewel dit een nieuw tijdperk inluidde waarin een elektronisch systeem potentieel kon leren, was er een belangrijk probleem met dit ontwerp: het kon alleen lineair scheidbare problemen oplossen. Terugkomend op de vroegere McCulloch-Pitts TLU, de eenvoudige AND, OR, NOT, en de NAND en NOR functies zijn alle lineair scheidbaar. Dit betekent dat een enkele lijn de gewenste uitgangen (ten opzichte van de ingangen) kan scheiden van de ongewenste uitgangen (figuur 4). XOR-functies (en de complementaire XNOR-functies) zijn anders. Wanneer de ingangen gelijk zijn (00 of 11), is de uitgang 0, maar wanneer de ingangen verschillend zijn (01 of 10), is de uitgang 1. Dit vereist dat de gewenste uitgang wordt ingedeeld in een groep ten opzichte van de ingangen. Eenvoudig gezegd: het perceptron kan niet worden getraind om te leren hoe XOR of XNOR werkt of om zijn functie te repliceren.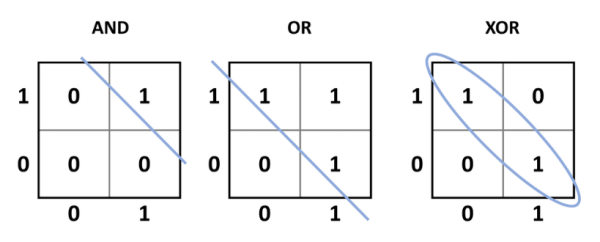
AND, OR, and XOR functions
Figuur 4: Van links naar rechts, de AND-, OR- en XOR-functies. De 1-uitgangen van de eerste twee kunnen
kunnen lineair, met behulp van een rechte lijn, worden gescheiden van de 0-uitgangstoestanden. Voor XOR kunnen de 1-uitgangen
niet lineair gescheiden worden van de 0-uitgangen, en dat is iets wat een
perceptron niet kan leren.
Het andere probleem lag bij de gebruikte activeringsfunctie. De lineaire drempelwaarde-eenheid maakte een scherpe sprong tussen inactief en actief zijn. Onderzoek dat resulteerde in het Delta Rule [6] netwerk toonde aan dat gradueel afnemend leren een cruciaal element was in het leerproces van neurale netwerken. Dit betekende ook dat elke activeringsfunctie differentieerbaar moet zijn. De plotselinge sprong van 0 naar 1 in de lineaire drempelwaarde-eenheid is niet differentieerbaar op het overgangspunt (de helling wordt oneindig), en de rest van de functie levert eenvoudigweg 0 (de output blijft onveranderd).

Voorgesteld werd dat een meerlaags netwerk met één of meer verborgen knooppunten tussen de in- en uitgangsknooppunten het XOR-probleem zou oplossen. Bovendien zou een differentieerbare functie, zoals de logistische functie (figuur 5), een sigmoïde curve, een soepele activeringsfunctie kunnen opleveren die het gradueel afnemend leren zou ondersteunen. De grote uitdaging was het leren -hoe zouden alle gewichten worden getraind?
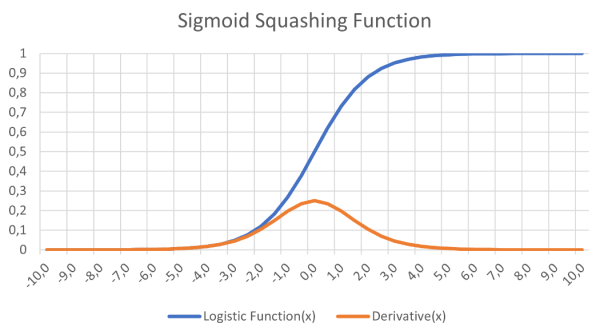
The logistic function pushes input values quickly towards either 0 or 1.
Figuur 5: De logistische functie duwt invoerwaarden snel in de richting van 0 of 1. Dit helpt
bij het leren van gradiënten in neurale netwerken.
De Delta Rule-benadering had aangetoond dat, door de fout in het kwadraat van het netwerk te berekenen (gewenste output - werkelijke output) en een leersnelheid toe te passen, de gewichten in het netwerk achtereenvolgens konden worden verbeterd totdat de optimale set gewichtsvectoren was gevonden (figuur 6). De toevoeging van een laag verborgen knooppunten tussen de input en de output maakte dit ingewikkelder te berekenen, maar niet onmogelijk, zoals we zullen zien.
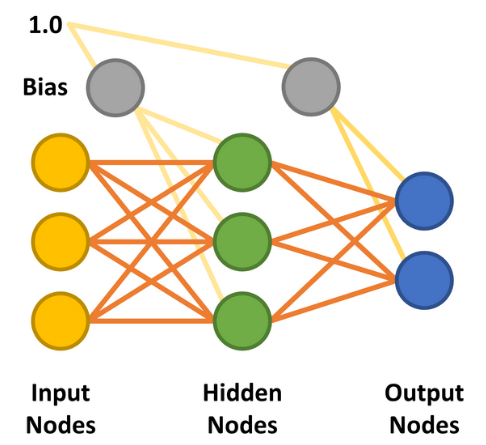
An example MLP with three input nodes, three hidden nodes, and two output nodes.
Figuur 6: Een voorbeeld MLP met drie invoerknooppunten, drie verborgen knooppunten, en
twee uitvoerknooppunten. De verborgen en uitvoerknooppunten kunnen een sigmoïdekromme gebruiken om
hun output te bepalen in de feedforward fase.

Meerlaags Perceptron

Met de toevoeging van de verborgen laag werd de meerlaags perceptron (MLP) mogelijk. De eenvoudigste vorm van een MLP neuraal netwerk maakt gebruik van één enkele verborgen laag. Alle knooppunten zijn met elkaar verbonden (bekend als 'fully connected'), waarbij gewichten worden toegekend tussen elk input- en verborgen knooppunt en tussen elk verborgen en output-knooppunt (figuur 7). De lijnen tussen de knooppunten stellen de gewichten voor. De gewenste inputs worden toegepast op de inputknooppunten (waarden tussen 0,0 en 1,0), en het netwerk berekent de respons van elk verborgen en outputknooppunt - een stap die bekend staat als de feedforward fase. Dit moet een resultaat opleveren dat aangeeft dat de inputwaarden overeenkomen met een outputcategorie die het netwerk heeft geleerd.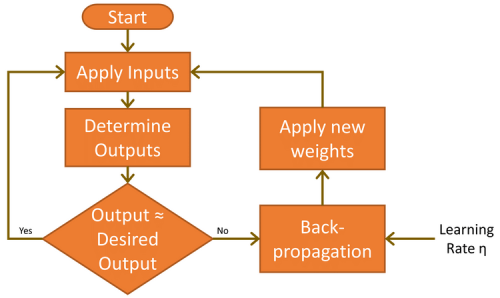
MLP function as flow diagram.
Figuur 7: Stroomdiagram dat laat zien hoe het leren van neurale netwerken wordt geïmplementeerd.
De inputs kunnen bijvoorbeeld worden gekoppeld aan een camera van 28 × 28 pixels die op handgeschreven getallen is gericht. De MNIST-database van handgeschreven cijfers die precies zulke beeldformaten bevat, zou de trainingsset kunnen vormen [7]. Elk van de uitgangen zou een van de getallen van 0 tot 9 voorstellen. Met het cijfer 7 voor de camera gehouden, zou elke uitgang de waarschijnlijkheid aangeven dat de input de waarde ervan is. Output 0 zal, hopelijk, aangeven dat het onwaarschijnlijk is dat het handgeschreven getal een 0 is, net als acht andere outputs. Maar output 7 zou een hoge waarschijnlijkheid moeten aangeven dat het handgeschreven getal 7 is. Eenmaal getraind, zou dit de verwachte functionaliteit moeten zijn voor een 7 uit de trainingsdataset of een nieuwe handgeschreven 7 die door een mens kan worden herkend.

Voordat dit kan gebeuren, moet het netwerk eerst de taak leren. Dit wordt bereikt door de input met handgeschreven 7's te 'voeren' en de resultaten van de output te analyseren. Aangezien het aanvankelijk onwaarschijnlijk is dat de resultaten correct zijn, wordt een leercyclus uitgevoerd om de gewichten zodanig te wijzigen dat de fout wordt verminderd. Dit iteratieve leerproces, dat bekend staat als backpropagatie, wordt vele duizenden malen uitgevoerd totdat de nauwkeurigheid van het netwerk voldoet aan de eisen van de toepassing. In de wereld van ML wordt dit 'supervised learning' genoemd.

Er zijn nog twee belangrijke factoren waarmee rekening moet worden gehouden in de feedforward en backpropagation fasen. De eerste is bias. Een bias-waarde van 1,0 vermenigvuldigd met een gewicht (tussen 0,0 en 1,0) wordt tijdens de feedforward-fase toegepast op de knooppunten van de verborgen en output-lagen. De bias heeft tot doel het probleemoplossend vermogen van het netwerk te verbeteren en duwt in wezen de logistische activeringsfunctie (zie figuur 5) naar links of rechts. De andere waarde is de leersnelheid, ook weer een waarde tussen 0,0 en 1,0. Zoals de naam al aangeeft, bepaalt dit hoe snel het MLP leert het gegeven probleem op te lossen, ook bekend als de snelheid van convergentie. Als de waarde te laag wordt ingesteld, zal het netwerk het probleem wellicht nooit met voldoende nauwkeurigheid oplossen. Te hoog ingesteld, loopt het netwerk het risico te oscilleren tijdens het leren en ook niet een nauwkeurig genoeg resultaat op te leveren (zie ook "Beperkingen van gradiënt-leren").

Het hier beschreven MLP kan worden beschouwd als een 'vanilla' ontwerp. Neurale netwerken kunnen echter op een groot aantal manieren worden geïmplementeerd. Deze omvatten meer dan één verborgen laag, het niet volledig verbinden van de knooppunten, het koppelen van latere knooppunten aan eerdere knooppunten, en het gebruik van verschillende activeringsfuncties [8].

Neurale netwerken: Beperkingen van Gradient Learning

Er zijn momenten waarop het neurale netwerk schijnbaar niet in staat is om te leren, ondanks dat het eerder de vereiste functionaliteit heeft geleerd met dezelfde knooppuntconfiguratie. Dit kan te wijten zijn aan het feit dat het netwerk blijft steken in een 'lokaal minimum' in plaats van een 'globaal minimum' van de foutfunctie te vinden.

MLP in Actie

Met het principe hopelijk duidelijk, zullen we nu een concreet voorbeeld bekijken. Het volgt op een uitstekend artikel van Matt Mazur, die veel tijd nam om backpropagatie uit te leggen in een MLP met een enkele verborgen laag [9]. Onze bespreking hier zal globaal zijn, maar geïnteresseerden (en niet bang voor wiskunde) wordt aangeraden Matt's stuk te bestuderen voor meer detail. Zodra het wiskundige werkingsprincipe is behandeld, zullen we een software MLP implementatie bespreken die werkt met dezelfde parameters als gebruikt voor deze theoretische analyse. Als je geïnteresseerd bent om mee te doen, is er een Excel spreadsheet die overeenkomt met Matt's uitgewerkte voorbeeld. Download of kloon gewoon de repository van GitHub [10] en kijk naar workedexample/Matt Mazur Example.xlsx in de map.

Om het eenvoudig te houden, wordt een twee-input, twee-output MLP met twee verborgen nodes gebruikt. De ingangsknopen zijn gelabeld i1 en i2, de verborgen knopen h1 en h2, en de uitgangsknopen o1 en o2. Voor deze oefening is het de bedoeling het netwerk te trainen om 0,01 uit te voeren op knooppunt o1 en 0,99 op o2 wanneer knooppunt i1 0,05 is en i2 0,10. Er zijn acht gewichten (w1 tot en met w8) en twee biaswaarden (b1 en b2). Om de wiskunde te kunnen repliceren, zijn aan alle ingangsknooppunten, biases en gewichten de waarden toegekend die in figuur 8 worden getoond en die overeenstemmen met het artikel van Matt Mazur.
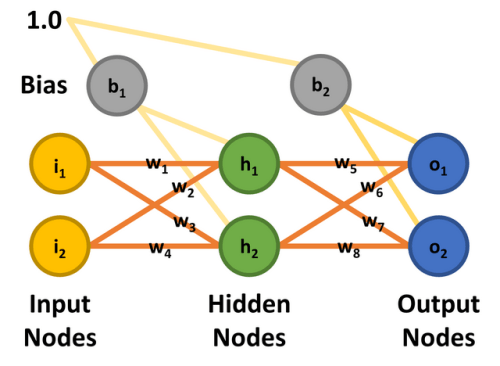
MLP example.
Figuur 8: MLP-configuratie gebruikt voor de voorbeeldberekeningen.

Feedforward

De feedforward fase om de outputs o1 en o2 te berekenen werkt als volgt. Elk verborgen knooppunt ontvangt een input die de netto som is van de inputs vermenigvuldigd met de gewichten, plus de bias-input (b1 = 0,35). Met behulp van het proces en de vergelijkingen van Matt Mazur is de input voor h1 de som van i1 vermenigvuldigd met w1 (0,15), i2 vermenigvuldigd met w2 (0,20) en b1 (0,35).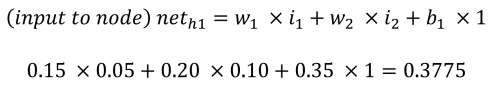
eq1 (Series on Neural Networks)
De outputwaarde van elke verborgen node wordt bepaald door de logistische (activerings)functie, waarbij de output van de verborgen node wordt afgevlakt tot een waarde tussen 0,0 en 1,0. Dit wordt als volgt berekend:
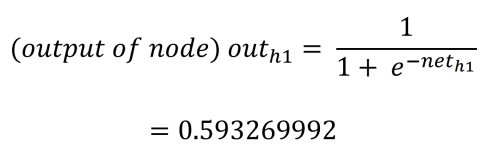
eq2 (Series on Neural Networks)
Door het proces voor h2 te herhalen (met w3 = 0,25, w4 = 0,3, en b1 = 0,35) krijgen we:
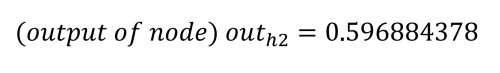
eq3 (Series on Neural Networks)
De netto-inputs naar de uitvoerknooppunten worden op dezelfde manier berekend, waarbij de berekende outputwaarden van de verborgen knooppunten worden gebruikt en de gewichten 5 tot en met 8 worden toegepast (w5  = 0,4, w6 = 0,45, w7 = 0,5, en w8 = 0,55) en de biaswaarde b2 = 0,60.
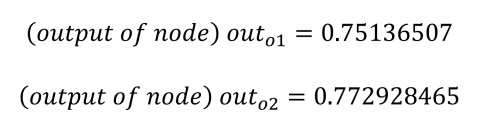
eq4 (Series on Neural Networks)
Zoals reeds gezegd, is ons doel om o1 0,01 uit te laten komen en o2 0,99, maar we zien dat we ver verwijderd zijn van dit resultaat. De volgende stap is het berekenen van de fout in elke uitgang met behulp van de foutkwadraatfunctie, en de totale fout als volgt:
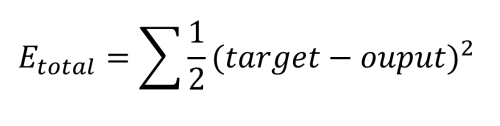
eq5 (Series on Neural Networks)
Deze wordt voor elke output als volgt berekend:
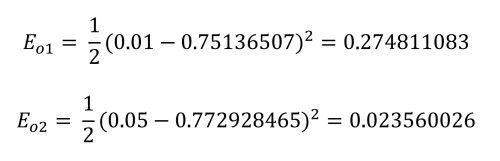
eq6 (Series on Neural Networks)
Tenslotte kan de totale fout voor het netwerk worden vastgesteld:
Equation 7 (Series on Neural Networks)
De volgende stap is om uit te zoeken hoe deze fout verbeterd kan worden.

Backpropagatie

Backpropagatie is waar het eigenlijke 'leren' gebeurt. Het proces bestaat hier uit het bepalen van de bijdrage die elk gewicht heeft op de totale fout. Eerst wordt gekeken naar de gewichten tussen de verborgen knooppunten en de uitvoerknooppunten. Wat de zaak ingewikkelder maakt, is dat w5 bijdraagt aan de totale fout via twee uitvoerknopen, o1 en o2, die ook worden beïnvloed door de gewichten w6 tot en met w8. Ook moet worden opgemerkt dat de bias-waarden geen rol spelen in deze berekeningen.

De wiskunde die nodig is om dit te definiëren is vrij ingewikkeld, maar het komt neer op enkele eenvoudige vermenigvuldigingen, optellingen en aftrekkingen. De berekening van de nieuwe waarde voor w5 , rekening houdend met de gekozen leersnelheid, η (0,5), gebeurt als volgt:
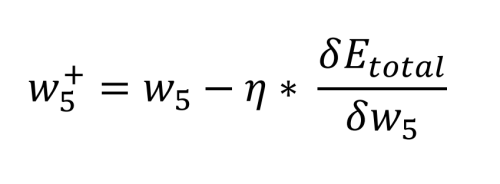
eq8 (Series on Neural Networks)
Hieruit kunnen wij de oude gewichten opnieuw bekijken en vergelijken met de nieuwe gewichten voor w5 tot en met w8:
eq9 (Series on Neural Networks)
Als we een snelle check uitvoeren, zien we dat dit logisch is. We willen dat o1 door w5 en w6 naar 0,01 wordt geduwd, en dat o2 door w7 en w8 naar 0,99 wordt geduwd.

De laatste stap is het bepalen van de bijdrage die de gewichten tussen de ingangen en de verborgen knooppunten hebben op de fout aan de uitgang. Zoals voorheen is de wiskunde beperkt tot eenvoudige vermenigvuldigingen, optellingen en aftrekkingen. In feite ziet de vergelijking er hetzelfde uit als die voor de berekening van de nieuwe gewichten w5 tot en met w8. Wat anders is, is hoe de totale fout ten opzichte van het gewicht (aanvankelijk w1) wordt berekend, aangezien de output van de verborgen laag afhankelijk is van een andere input en een ander gewicht (zowel voor h1, i1 en w1 als voor i2 en w2):
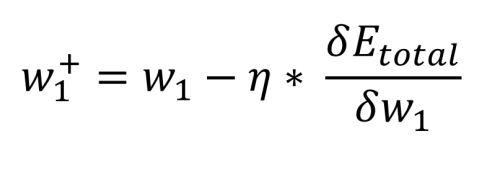
eq10 (Series on Neural Networks)
Ook bij deze berekening speelt de biaswaarde geen rol. Nu kunnen we de oude gewichten w1 tot en met w4 vergelijken met de nieuwe gewichten:
eq11 (Series on Neural Networks)
Nu de nieuwe gewichten zijn bepaald, kunnen de oude gewichten worden vervangen door de nieuwe gewichten en kan een nieuwe forward pass worden uitgevoerd. Zolang de uitgangsfout groter blijft dan gewenst, kunnen backpropagatie-passages worden herhaald zoals hier beschreven.

MLP Implementatie in Processing

Om dit eenvoudige neurale netwerk te demonstreren, werd een neuraal netwerk vanaf nul gecodeerd als een klasse die kan worden gebruikt in Processing [11], de ontwikkelomgeving die is ontworpen voor het bevorderen van coding binnen de beeldende kunsten. De visuele mogelijkheden van de IDE maken het mogelijk om 2D en 3D afbeeldingen gemakkelijk weer te geven. Een tekstconsole maakt het ook mogelijk ideeën snel en gemakkelijk te testen. De code die volgt is onderdeel van het genoemde repository [10].

De code voor de MLP implementatie is te vinden in de map processing/neural/neural.pde. Dit bestand hoeft alleen maar te worden toegevoegd aan elk Processing-project dat het wil gebruiken. De Neural-klasse kan worden ingesteld om elk gewenst aantal invoer-, verborgen- en uitvoerknooppunten te ondersteunen. Om het reeds besproken voorbeeld te herhalen, moet het bestand processing/nn_test/nn_test.pde nu geopend worden in Processing.

Het creëren van een neuraal netwerk is vrij eenvoudig. Eerst wordt de klasse constructor Neural(in nn_test.pde) aangeroepen om een object te creëren, hier networkgenaamd, met het gewenste aantal ingangen, verborgen knooppunten, en uitgangen (2, 2, en 2). Eenmaal gecreëerd, worden verdere functies aangeroepen om de leersnelheid en de biases van de verborgen node en de output node in te stellen, zoals in de voorbeeldschets.

De constructor initialiseert ook de gewichten met willekeurige waarden tussen 0,25 en 0,75. Om overeen te komen met het voorbeeld, wijzigen we de gewichten zoals getoond in Listing 1, waar ook de invoerwaarden en de gewenste uitvoerwaarden zijn gedefinieerd.
Using the MLP Neural class in nn_test.pde. (Series on Neural Networks)
Listing 1: Gebruik van de MLP Neurale klasse in nn_test.pde.
De voorbeeldcode laat ook een verbose-mode toe waarmee de werking voor elke stap van de berekeningen kan worden getoond. Deze moeten overeenkomen met de resultaten in de Excel-spreadsheet.

Na het klikken op Run in Processing, zou de tekstconsole het volgende moeten weergeven:


...forwardpass complete. Results:

For i1 =  0.05  and i2 =  0.1

o1 =  0.75136507  (but we want:  0.01 )

o2 =  0.7729285  (but we want:  0.99 )

Total network error is:  0.2983711
 

Hierna wordt ‘learning’ ingeschakeld en wordt opnieuw een forward pass uitgevoerd, gevolgd door de backpropagation stap. Dit resulteert in de output van de nieuwe en oude gewichten en de berekening van een nieuwe forward pass om de nieuwe output node waarden en fouten te bepalen:

New Hidden-To-Output Weight [ 0 ][ 0 ] = 0.3589165, Old Weight = 0.4

New Hidden-To-Output Weight [ 1 ][ 0 ] = 0.40866616, Old Weight = 0.45

New Hidden-To-Output Weight [ 0 ][ 1 ] = 0.5113013, Old Weight = 0.5

New Hidden-To-Output Weight [ 1 ][ 1 ] = 0.56137013, Old Weight = 0.55

New Input-To-Hidden Weight[ 0 ][ 0 ] = 0.14978072, Old Weight = 0.15

New Input-To-Hidden Weight[ 1 ][ 0 ] = 0.19956143, Old Weight = 0.2

New Input-To-Hidden Weight[ 0 ][ 1 ] = 0.24975115, Old Weight = 0.25

New Input-To-Hidden Weight[ 1 ][ 1 ] = 0.2995023, Old Weight = 0.3



We kunnen zien dat deze de gewichten 5 tot en met 8 vertegenwoordigen en daarna 1 tot en met 4. Zij komen ook overeen met de eerder gemaakte handberekeningen (met kleine uitzonderingen als gevolg van afrondingsfouten).

Volgende stappen met MLP en meer over neurale netwerken

Wil je meer leren over neurale netwerken? Na een goed begrip van de werking van een MLP neuraal netwerk en de voorbeeld Neural-klasse die hier voor Processing wordt gegeven, kan de lezer zelfstandig verdere experimenten uitvoeren. Enkele ideeën zijn:
 
  • Laat het leren in een lus lopen - Hoeveel epochs zijn nodig om een netwerkfout van 0,001, 0,0005, of 0,0001 te bereiken?
  • Start met verschillende biases en gewichten - Welke invloed heeft dit op het aantal epochs dat nodig is om te leren? Lukt het het neurale netwerk ooit niet om te leren?
  • Map outputs naarinputs - Probeer een 3D-plot te genereren van elke output tegen de inputs zodra het netwerk zijn taak heeft geleerd. Ziet het eruit zoals je zou verwachten? Misschien wil je liever Plotly's Chart-Studio gebruiken in plaats van een spreadsheet [12] om de uitvoergegevens te plotten.


In het volgende artikel in deze serie over neurale netwerken zullen we ons neurale netwerk leren hoe logische poorten te implementeren en het leerproces te visualiseren.

Heb je vragen of opmerkingen over neurale netwerken of over iets anders dat in dit artikel is behandeld? Stuur dan een e-mail naar de auteur op stuart.cording@elektor.com.